[Classical Mechancis] Double pendulum problem code

1. Differential equations [1]

Please read an article on the following website if you want to know the differential equations used in this code.  https://scipython.com/blog/the-double-pendulum/

2. Methods & Language

1. Methods: 4th order Runge-Kutta methods  
2. Programming Language: C code 

3. Code

#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>

struct particle {
	double x;    // generalized coordinate (in this problem, theta) 
	double vx;   // generalized velocity 
};

const double m1 = 1.;                                  // the mass of the particle 1
const double m2 = 1.;                                  // the mass of the particle 2 
const double g  = 9.81;                                // the gravitional acceleration
const double l1 = 1;                                   // the length of the rod 1
const double l2 = 1.;                                  // the length of the rod 2 
const double RK4_C1[4] = {0, 0.5, 0.5,1};              // Runge-Kutta coefficient 1  
const double RK4_C2[4] = {1./6, 1./3., 1./3.,1./6.};   // Runge-Kutta coefficient 2 
const double dt = 1.1235710e-5;                        // the increment of time 
const double pi = 3.1415926535;                        // numerical value of pi
const double TMAX = 100;                               // max time 
const double initial1[2] = {pi / 2.0, 0.0};            // initial condition for particle 1 
const double initial2[2] = {pi / 2.0, 0.0};            // initial condition for particle 2 

//###############################################################
//  DECLANATION OF FUNCTIONS 
//###############################################################
double acc_th1(double th1, double th2, double v_th1, double v_th2);
double acc_th2(double th1, double th2, double v_th1, double v_th2);
void RK4_diff_eq(struct particle  *mass1, struct particle *mass2);

//###############################################################
//  MAIN FUNCTION
//###############################################################
int main(void){

	struct particle mass1 = {initial1[0], initial1[1]};
	struct particle mass2 = {initial2[0], initial2[1]};
	int maxiteration = TMAX / dt, n = 0;
	double t = 0;
	FILE *data = fopen("double_pendulum_problem.dat", "w");
	fprintf(data, "#%10s %10s %10s %10s %10s \n", "time", "theta1", "theta2", "v_theta_1", "v_theta_2");
	
	while( n < maxiteration ){	
		RK4_diff_eq(&mass1, &mass2);
		n ++; 
		if (n % 100 == 0){
			fprintf(data, "%10f %10f %10f %10f %10f \n", dt * n, mass1.x, mass2.x, mass1.vx, mass2.vx);
		}
	};
	fclose(data);
	return 0;
}

//#############################################################
// DEFINITION OF FUNCTIONS 
//#############################################################

double acc_th1(double th1, double th2, double v_th1, double v_th2){
	return 
		(m2 * g * sin(th2) * cos(th1 - th2) - m2 * sin(th1 - th2) * (l1 * (v_th1 * v_th1 ) * cos(th1 - th2) + l2 * (v_th2 * v_th2)) - (m1 + m2) * g * sin(th1))/
		(l1 * (m1 + m2 * pow(sin(th1 - th2), 2)));
}
double acc_th2(double th1, double th2, double v_th1, double v_th2){
	double d_th = th1 - th2;
	return 
		((m1 + m2 ) * (l1 * (v_th1 * v_th1) * sin(d_th) - g * sin(th2) + g * sin(th1) * cos(d_th)) + m2 * l2 * (v_th2 * v_th2) * sin(d_th) * cos(d_th))	/
		(l2 * (m1 + m2 * pow(sin(th1 - th2), 2)));

}
void RK4_diff_eq(struct particle  *mass1, struct particle *mass2){
	
	double th1, th2, vth1, vth2, n_th1, n_th2, n_vth1, n_vth2;
	double kvth1 = 0, kvth2 = 0, kth1 = 0, kth2 = 0;
	
	th1  = mass1->x;
	th2  = mass2->x;
	vth1 = mass1->vx;
	vth2 = mass2->vx;

	n_th1 = th1;
	n_th2 = th2;
	n_vth1 = vth1;
	n_vth2 = vth2;


	for (int n = 0; n < 4; n ++){
		double c1 = RK4_C1[n], c2 = RK4_C2[n];
		kvth1 = acc_th1(th1 + c1 * kth1, th2 + c1 * kth2, vth1 + c1 * kvth1, vth2 + c1 * kvth2) * dt;
		kvth2 = acc_th2(th1 + c1 * kth1, th2 + c1 * kth2, vth1 + c1 * kvth1, vth2 + c1 * kvth2) * dt;
		kth1  = dt * (c1 * kvth1 + vth1);
		kth2  = dt * (c1 * kvth2 + vth2);
	
		n_th1  += c2 * kth1;
		n_th2  += c2 * kth2;
		n_vth1 += c2 * kvth1;
		n_vth2 += c2 * kvth2;
	}
	mass1->x  = n_th1;
	mass1->vx = n_vth1;
	mass2->x  = n_th2;
	mass2->vx = n_vth2;

}

 

4. Results 

1) for the following initial conditions;

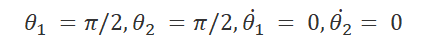
2) Results

0

Double Pendulum